As mentioned in my first blog post, one of the main reasons I decided to develop a sudoku app was a fascination with how they were generated. It puzzled me for quite some time, as I tried to come up with my own solution. When I started work on the project, I was able to research different methods for board generation, and I was quite surprised by what I found. As it turns out, the most popular method is to just hand over an empty board to a solving algorithm, and see what it comes up with. Thats it! I thought there would be something much more efficient, as I wasn’t considering just how fast a solving algorithm can be.
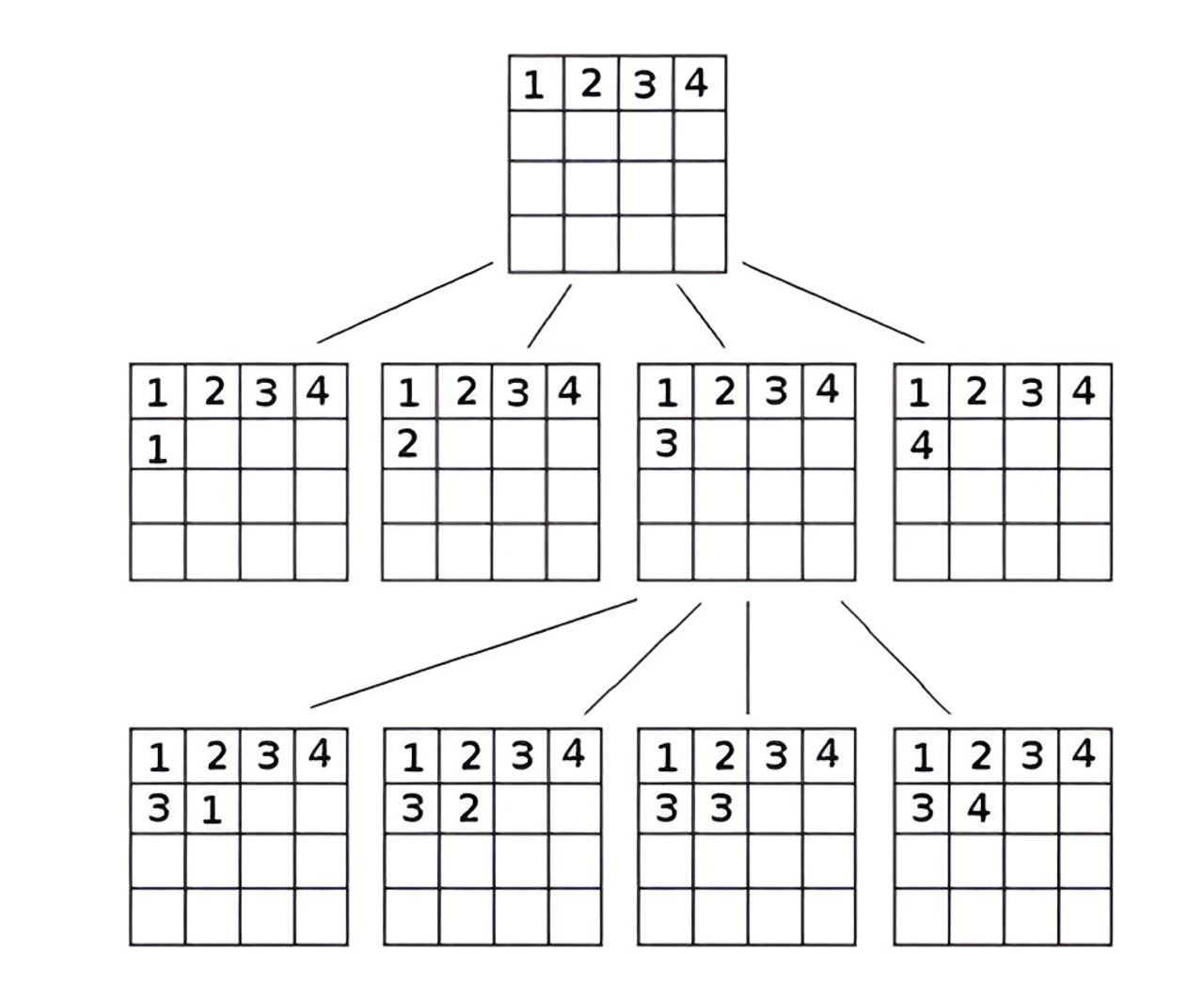
But that’s only half the problem. After generating the completed board, you need to remove cells to create the puzzle. You could remove a given number of tiles at random, but there’d be no guarantee the puzzle would have only 1 solution. You might as well just give them an empty board! In fact, you can have multiple solutions with as little as 4 cells removed. So to ensure there’s only 1 solution, you need to again use a solving algorithm, and backtrack whenever multiple solutions are found.
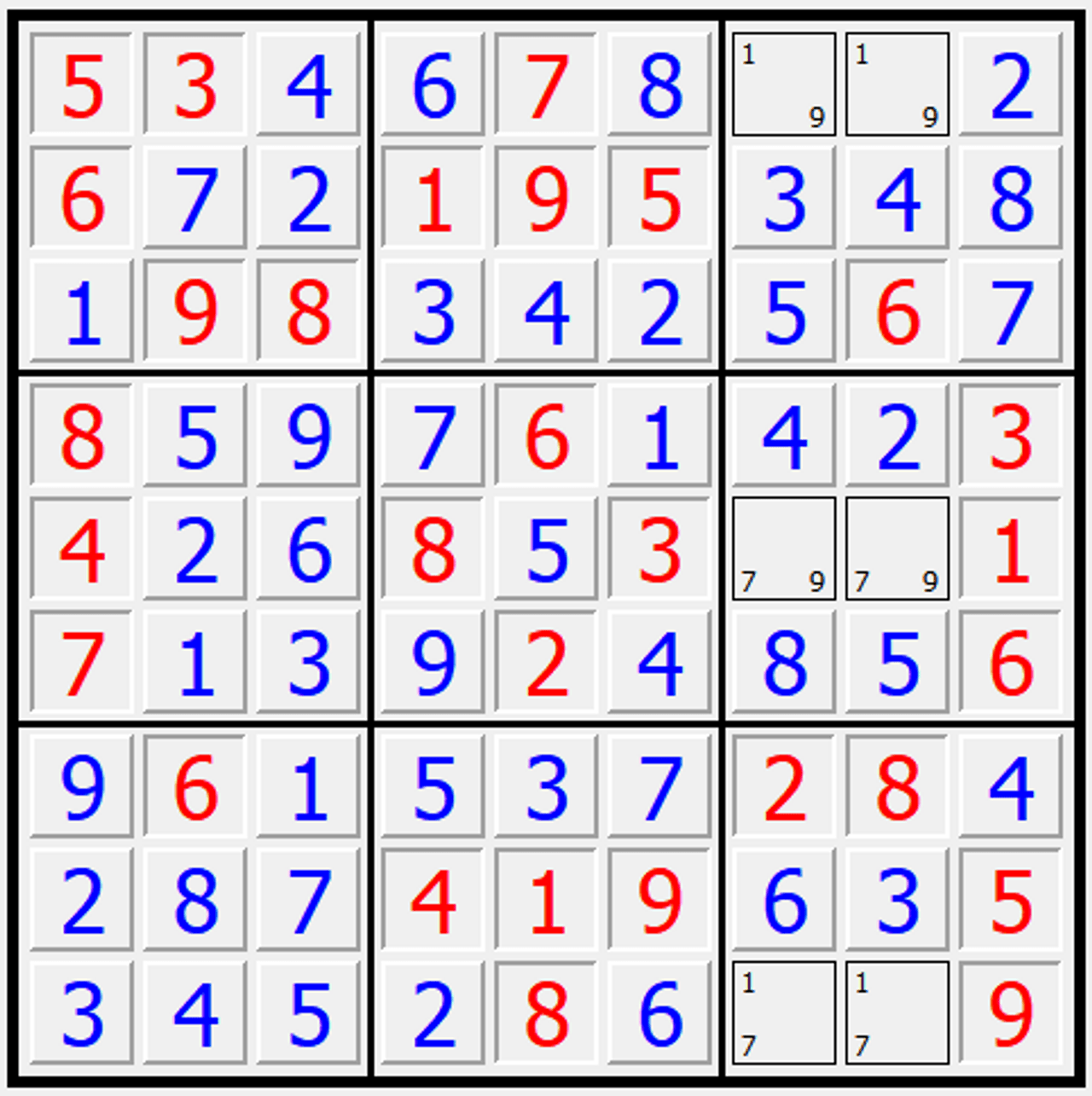
That’s pretty much where my app stands today. The solving algorithm I implemented uses backtracking & branch pruning, finding a cell with the smallest number of candidates (as seen below), and trying out each candidate in a random order. It backtracks whenever a cell is found with no candidates.
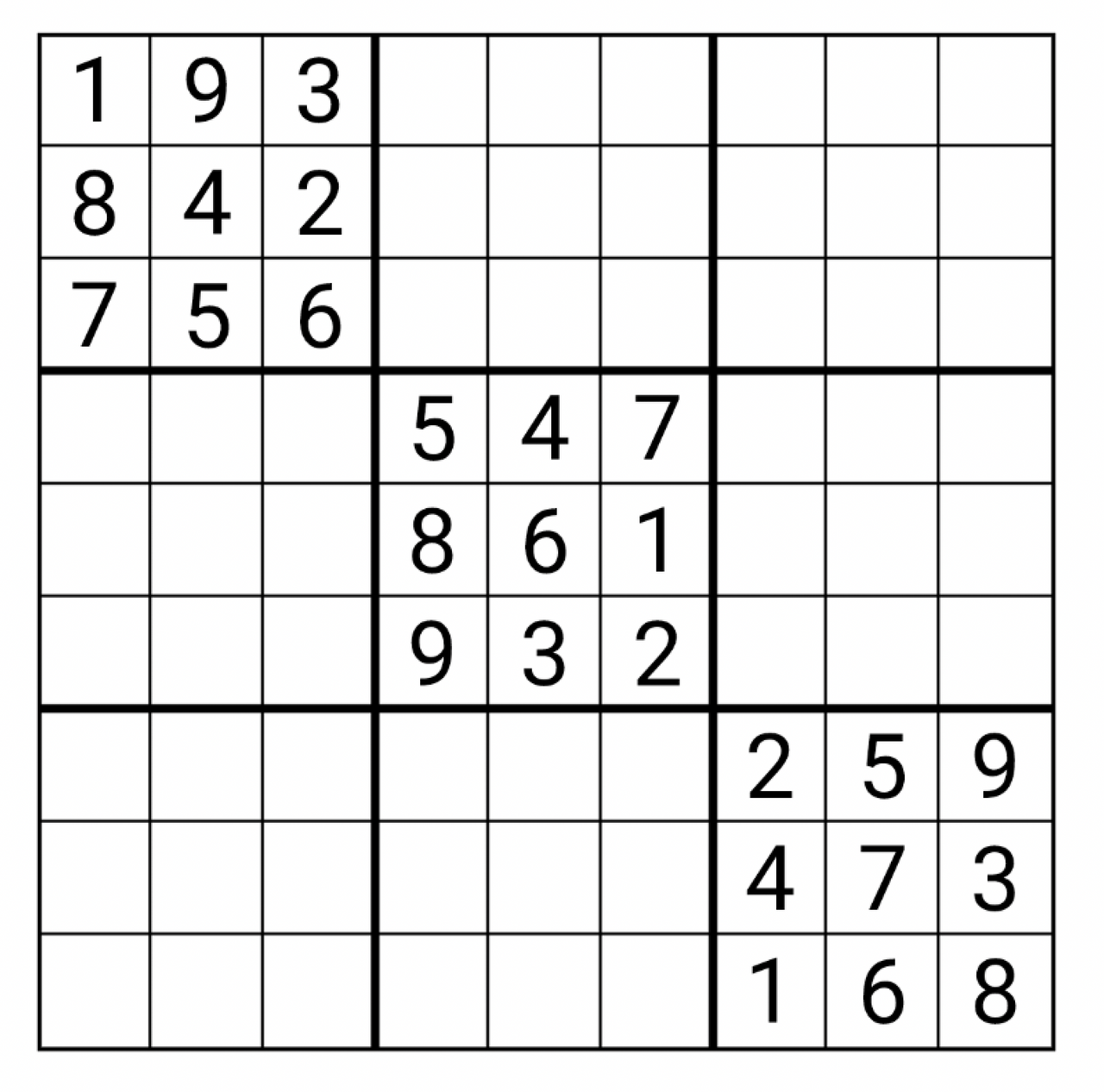
I also don’t start from a completely empty board. Since the top-left, middle, and bottom-right blocks never intersect, I fill each of them in with numbers 1-9 at random, then begin from there.
So far, every time we’ve tried to improve the quality of the sudoku, its become much harder to implement. Of course, the easiest approach is to fill in a few cells with numbers at random, but there may not even be a valid solution in this case. A backtracking solving algorithm can generate a complete board, but removing cells at random doesn’t guarantee one solution. An additional backtracking removal algorithm can guarantee a single valid solution. What more could be improved upon?
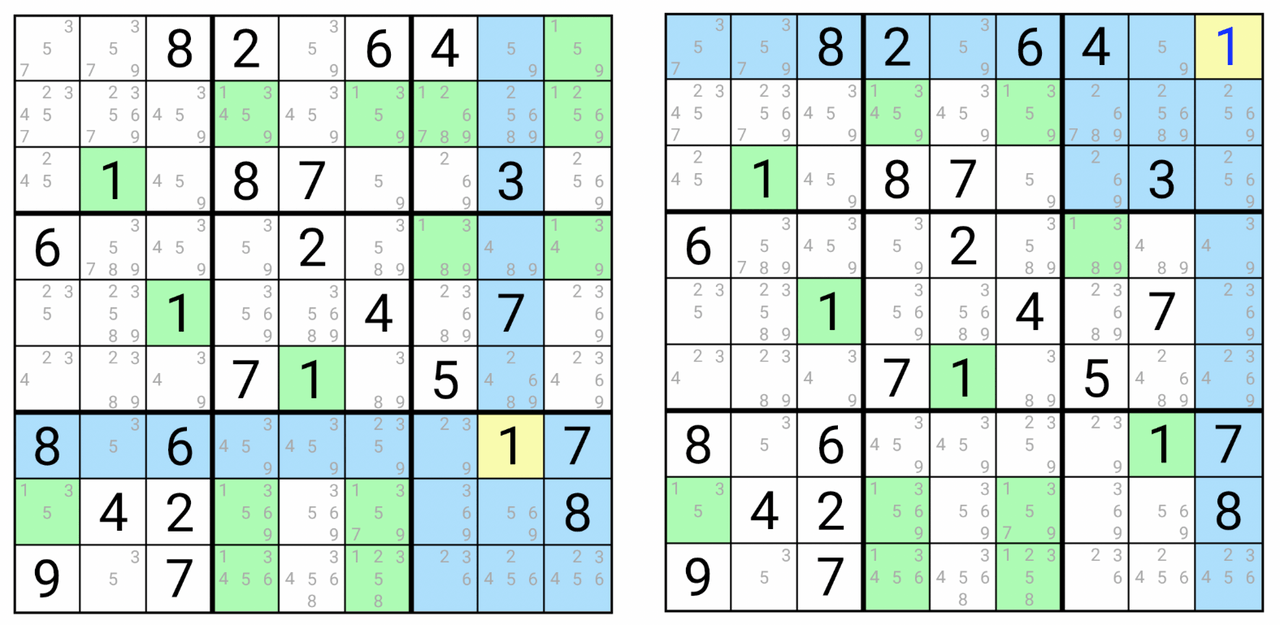
Well, after playing some puzzles in my app, I noticed they kinda sucked. In fact, I added a ‘hint’ button, whose only purpose is to fill in any cell which has only one candidate, or is the only location for a candidate in a row, column, or block. Through spamming the hint button, I was able to complete the highest difficulty puzzles over half the time.
The issue is that the number of cells to remove isn’t a very good indicator of difficulty. It’s easy to implement, and feels like it should produce harder puzzles, but when the computer is removing cells, getting rid of a number which has to go in that location will never produce more solutions. It’s much harder to find a cell which won’t produce more solutions, but can’t be immediately replaced. Even if a cell like this is found, it may lose this status once the cells removed before it are replaced. Basically, there are just many more easy puzzles that can be created than difficult ones, so when we just return the first board found with only one unique solution, it’s much more likely to have a trivial solution.
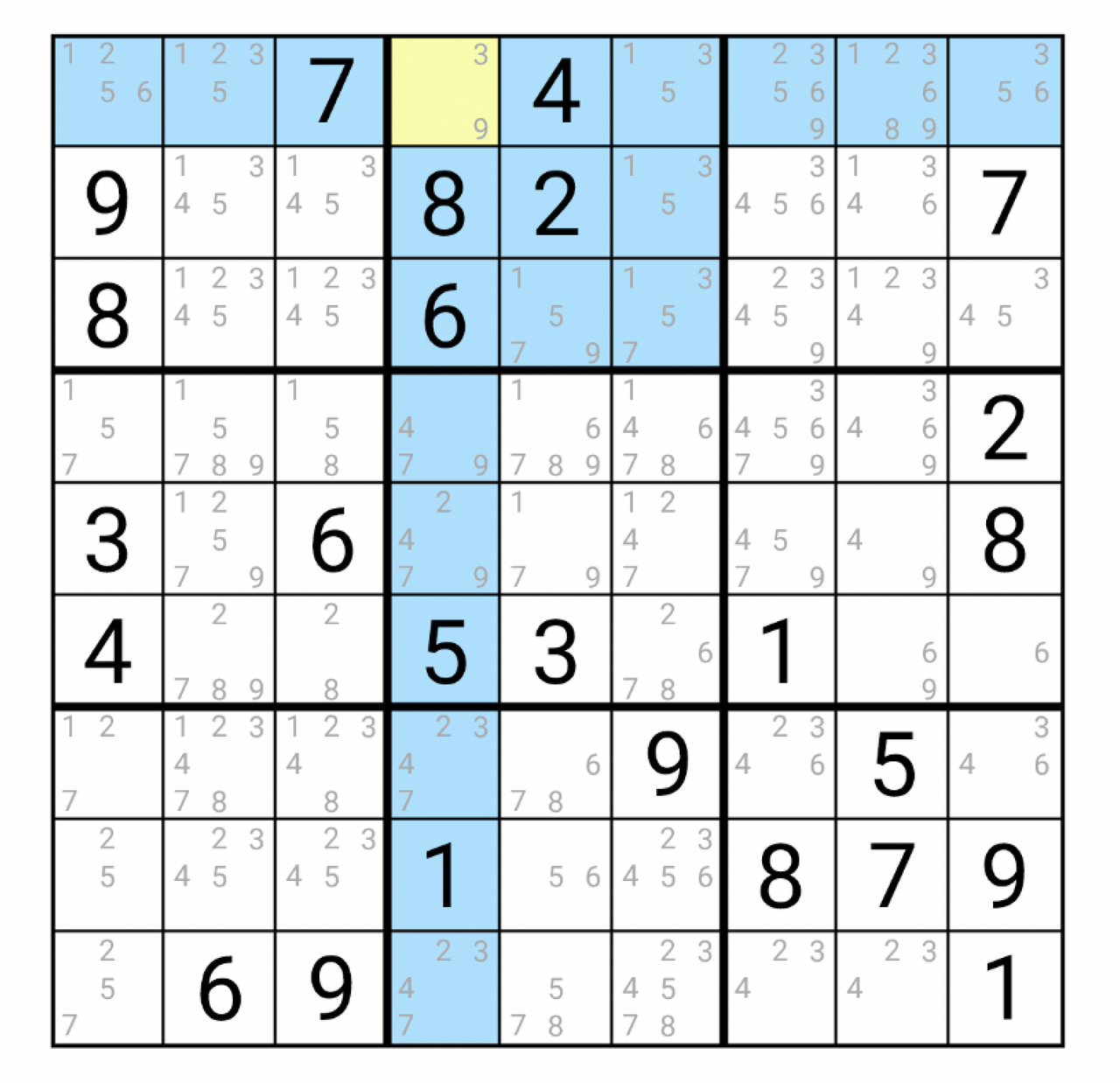
All hope is not lost, however. I’ve started work on a system which can get aroung this issue. Rather than removing a given number of cells, the cell removal algorithm could aim for a certain difficulty rating. Then, instead of using the solving algorithm used to generate the board, it can use techniques implemented by humans to solve the puzzle. Each technique will have its own difficulty level attached, and the rating of the puzzle is based on the sum of these scores. At each point, the app will seek out the easiest technique first. This won’t necessarily find the minimum difficulty rating possible, but that’s fine, it’s a good enough heuristic to get the gist.
This last method will certainly take me more time to implement. Implementing just a few techniques is difficult & time consuming, and there’s a lot of techniques, with increasing complexity. For now, I’m focusing on other aspects of the program, hoping to get the game released, but I’ve found this fascinating to research, and can’t wait to finish it!
Check it out on GitHub to follow development.